Two-Sector Growth: |
 |
Let us summarize what we have found. Remember that the Uzawa two-sector growth model poses two essential questions: (1) can we guarantee a unique factor-market equilibrium w for every capital-labor ratio k? (2) can we guarantee that k approximates a steady-state growth path k* over time? We have found sufficient conditions for (1) and (2).
In Uzawa's (1961) Classical hypothesis case (all wages spent, all profits saved), the sufficient condition for (1) was that the Uzawa capital-intensity condition hold true (i.e. that the consumer goods industry is more capital-intensive that the investment goods industry). This, as we saw intuitively, was also sufficient to guarantee uniqueness and stability of the steady state (i.e. sufficient for (2)).
In the more flexible savings case, we found that a sufficient condition for (1) was that sr = sw = s (Uzawa's (1963) savings condition). Another sufficient condition (stated, but not proved) was that sr > sw and kc > ki and still another was that sr < sw and kc < ki (the Drandakis's (1963) mixed conditions). To guarantee (2), we must add the Uzawa capital-intensity assumption to Uzawa's savings condition (not shown, but deducible). Alternatively, we have shown that the first of Drandakis' mixed conditions is also sufficient for (2).
Of course, all the conditions we have outlined thus far are all sufficient conditions for stability, but not necessary conditions. In other words, other configurations of savings and capital-intensity could yield us uniqueness and/or stability, but it these would by no means be guaranteed.
It might be useful, then, to consider cases where we have indeterminacy and instability with other configurations. Examples are given by, among others, Uzawa (1963) and Inada (1963). An interesting case is the possibility of cycles. Specifically, consider Figure 8, effectively a reproduction of the differential equation we had in Figure 7, but now with arrowheads included to indicate direction. Recall that this was obtained from a factor market equilibrium locus k(w) which was not monotonic (see Figure 6).
In Figure 8, there are two steady-states, b and d. Immediately, we have indeterminacy of steady-state equilibrium as either could obtain. It is immediately noticeable that both steady states b and d are locally unstable, in the sense that any slight nudge away from them and we will return to them. Thus, we have no stable steady-states. At k0, we also have indeterminacy of factor market equilibria: points a, b and c are all possible factor market equilibria at k0. There is no reason to accept one over the other.

Fig. 8 - Indeterminacy and Cycles
A cycle can be traced from the passage along the points (1, 2, 3, 4). Specifically, suppose we begin at point c, with capital stock k0 and factor price equilibrium represented by c. In this case, dk/dt < 0, and so the capital-labor ratio declines below k0. We continue declining until we reach kL (point 1 in Figure 8). At kL, we still have it that dk/dt < 0, so there will be a tendency to continue to reduce k. But notice that the slightest reduction in k below kL leads to an immediate jump from point 1 to point 2, i.e. there is a catastrophic jump from dk/dt < 0 to dk/dt > 0.
Thereafter the capital-labor ratio begins rising from kL towards k0. At k0, however, we will be at factor equilibrium point a: we have no reason to jump down towards b to get steady-state. But staying at a implies that dk/dt > 0, so k continues to rise. It will do so until we reach kU. At this capital-labor ratio, a slight increase in k will lead to an immediate catastrophic jump from point 3 to point 4, and thus a drastic reversal from dk/dt > 0 to dk/dt < 0 around kU. Now, the capital-labor begins falling, from kU towards k0. But at k0, we will have the factor market equilibrium implied by c, and not b. Thus, we continued declining towards kL.
Thus, as we see in Figure 8, we have a constant cycle fluctuating back and forth between kL and kU, passing over k0 in the process but never actually stopping there because the steady-state factor market equilibrium b never gets the chance to realize itself.
How anomalous is this case? Inada (1963) provides a precise example of the kind of cyclical behavior we see. Naturally, none of the uniqueness conditions we imposed above hold here -- e.g. Uzawa's capital-intensity assumption must have been violated in order to obtain this kind of differential equation. Uzawa (1963) considered the possibility of cycles. He noted that the kind of jumps required (from 1 to 2, from 3 to 4) implied discontinuous jumps in the factor price equilibria. What if these were not accommodated? In other words, what if we forced factor prices to adjust only slowly? This requires that we allow for unemployment of capital and/or labor for extended periods of time. This modification will not be pursued here.
An interesting consideration is the Uzawa savings hypothesis, sw = sr = s. This was, as we noted earlier, sufficient to rule out multiple factor-market equilibria. But, in and of itself, it does not rule out multiple steady-states. Specifically, we could still have the case depicted in Figure 9, where although we only have one factor-market equilibrium for every k, nonetheless we have three steady-state capital-labor ratios, k1, k2 and k3. We will have alternating stable/unstable capital-labor ratios (k1 and k3 are stable, and k2 unstable). But this might not really matter too much: from any initial k, we will approach some steady-state. For instance, in Figure 9, if we begin with a capital-labor ratio smaller than k2, we will approach k1 over time; if our initial k is greater than k2, then we will approach k3.
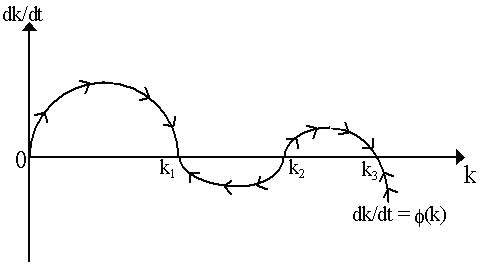
Fig. 9 - Multiple Steady-States
However, if we were to impose the Uzawa capital-intensity condition on top of the Uzawa savings assumption, then Figure 9 could no longer hold: we would have uniqueness and stability of steady-state equilibrium.
Figure 9 has an even more interesting implication as it is almost directly comparable to the Solow-Swan (one-sector) growth model. We obtain Figure 9 by assuming the same savings propensity out of wages and profits, so there is only one savings rate in the economy, s = sw = sr, just like in Solow-Swan! Now, we don't have the complications of multiple factor-market equilibria, but we do have the complications of multiple steady-state growth paths. In Solow-Swan this never happened: steady-state was always unique. However, even though all the main assumptions are the same, the two-sector model yields a qualitatively different result.
There are other modifications to the standard Uzawa two-sector model. For instance, Drandakis (1963) endogenized the labor supply by making it responsive to wages (thus getting actually closer to the Classical way of thinking). Morishima (1969) did the same, but found that the Uzawa capital-intensity condition was no longer sufficient for stability.
No less interestingly, Joseph Stiglitz (1967) has allowed capital to be owned by explicitly different capitalist-worker classes and analyzed the consequent implications. Adopting the savings assumptions from Pasinetti (1962), specifically that the savings propensity of capitalists exceeds that of workers, then he found that the Uzawa capital-intensity assumption is sufficient for uniqueness of factor market equilibrium and also sufficient for the uniqueness and stability of steady-state growth path. However, for existence of a steady-state path at all, it is necessary and sufficient that the savings rate of workers is less than the ratio of investment to output.
Other modifications include the following. Yasui and Uzawa (1964) make capital depreciation endogenous. Inada (1966) introduced fixed capital which cannot be transferred from one use to another. Two-sector models with fixed proportions technology, as noted, have also been considered by Y. Shinkai (1960) and John Hicks (1965). Inada (1963) has allowed for the savings rate itself to be a function of income, so s = s(y).
Technological change has been one of the bigger headaches because now we must ensure that technological change is such that all sectors grow at the same rate. Diamond (1965) and Takayama (1965) developed a classification scheme is analogous to the one-sector case where we have Harrod-neutral technical change where there is constant capital per effective labor unit in each sector as well as in the aggregate. Charles Kennedy (1962) proposed a different type of neutral technical progress where it is the value of capital per labor unit that remains constant, which has different implications. We consider this elsewhere.
Finally, we should try to decipher the main lesson from all this. Robert Solow claims that it "seems paradoxical to me that such an important characteristic of the equilibrium path [i.e. stability] should depend on such a casual property of the technology." (Solow, 1961). Perhaps it is not that paradoxical. As Frank Hahn notes, the Uzawa capital-intensity condition and attendant savings hypotheses "are all terrible assumptions" (Hahn, 1965) which probably never or only rarely hold in the real world. It is thus reasonable to conclude from this exercise that, if anything, these models have taught us that the real world is a bit more complicated than one-sector models let on. Rather than the smooth convergence to a single steady-state path we find in the Solow-Swan model, the Uzawa two-sector model indicates that we ought to expect a good amount of indeterminacy, instability and cyclical behavior in growth paths. Now that sounds a little bit more like the world we live in.
The famous "optimal growth" extension of the two-sector model by Uzawa (1964) and Srinivasan (1964), which tries to introduce some more determinacy into the result shall be considered in the next section.